Polyhedral Globes

Paper Polyhedra

I’ve wanted for a long time to create ways to make spheres out of paper. The “celestial sphere” of stars, the globes of the earth and moon, maps of the earth at various times and in various conditions — it could be such a fun and useful activity to be able to work with paper models of all these things. Some time back, I worked out a way to make paper hemispheres, as you can see in my paper celestial spheres, but these have their pros and cons. Another strategy would be to cut and fold a piece of paper into a shape that resembles a sphere, but is made up of lots of small flat surfaces instead of one big curved surface. In other words, we could model a sphere as a polyhedron. It's not too hard to create a design on paper to cut out and fold into a polyhedron, and with a little fancy math and a good source image, it's possible to draw maps on these polygonal faces, so that they make a globe when you fold them into shape.

Four of the simplest polyhedra are the cube, the octahedron, the dodecahedron, and the icosahedron. The cube and the octahedron don’t resemble a sphere very well, but I thought I’d try making globes out of them all just for fun and for comparison. I found that the cube is actually not quite as goofy as I thought it would be — it gives you broad uninterrupted flat maps to study, and still keeps all the parts of the world in relatively good relative arrangement. The octahedron is too pointy. My favorite shape for a polyhedral globe is a toss-up between the dodecahedron and the icosahedron. The icosahedron is fairly easy to make, and it resembles a sphere better than the others. But the poles are pointy, and I find all those faces and edges to be a little distracting to the eye. It’s too easy to focus on the shape rather than the map. The dodecahedron is the most bothersome to make, but it gives broad maps to study, and the poles are flat, which I like visually, and it also allows you to rest the globe in a straight up-and-down position. This is one of those issues where I expect different people will have different preferences. For most of the following downloads, I have created both dodecahedral and icosahedral versions.

In all of the downloads presented here, the cut lines are thick and black, and the fold lines are thin and gray. As usual, I recommend printing the designs onto card stock, and scoring the fold lines with a dull edge of some kind before cutting out the shapes to help make crisp folds. Folding the paper into shape should be relatively straightforward — just make sure the imagery is on the outside and the tabs are on the inside. I recommend gluing the tabs in place with glue sticks rather than taping with scotch tape. The results are prettier and more sturdy. Unfortunately, gluing the final tabs in place is always a bit awkward. Liquid glue helps here. Perhaps some day I'll think of a way to make glue-less interlocking tabs somehow.

If you want to make your own designs, or are interested in plain, undecorated paper polyhedra for whatever reason, here are the same shapes without the maps:

For those with a passion for polyhedra, you can find a cornucopia of other makable paper shapes at polyhedra.net.

Celestial Spheres

One of the main motivating factors for me to work on these polyhedra was so that I could make paper celestial spheres, so naturally I created celestial sphere versions of my polyhedra. There are two versions here, one inside-out, and one ‘normal’. The trouble with making globes to represent the map of constellations surrounding us, is that we are inside this ‘celestial sphere’, looking at it from the interior. When we make an artificial model, a physical globe of some kind, we are normally on the outside looking in. So with the celestial sphere, we have a choice. We can draw everything on the globe ‘properly’, and then either try to find a way to view it from the inside, or look at it from the outside and just put up with having all the constellations look backwards. Or we can draw the celestial sphere ‘backwards’ to start with, so that the constellations would look reversed if we were actually on the inside, but they will look ‘right’ when we look at them from the outside.

The second of these two dodecahedra is drawn without the outer tabs, and is meant to be folded so that the stars are on the inside. The result after fastening the tabs in place (on the outside—this is an exception to the normal rule) will be a sort of ‘clamshell’ that can open and close, and let you look at the stars from the ‘inside’. The first is meant to be folded and fastened just like all the other dodecahedra here, making a complete sphere, with the stars on the outside.

If you don't mind using up all of the black toner in your printer, you might also want a celestial sphere that captures the beauty of a deep, dark, rich night sky. I made the following celestial spheres, in which you can see the Milky Way and the Magellanic Clouds, using some “deep sky” imagery from NASA. In the first set of celestial spheres, the spheres are oriented “normally”, with the Celestial North Pole (very near to the North Star) at the top, the Celestial Equator (which runs through Orion's Belt) around the middle, and the Celestial South Pole at the bottom. If you make these, the North Star and the North Pole will be aligned with one “pole” of the polyhedron, and the South Pole will be aligned with the opposite “pole” of the polyhedron.

In this second set, I oriented the spheres with the “Galactic Plane”, so that the Milky Way runs around the middle, and the “Galactic Poles” are at the top and bottom. (The North Galactic Pole is in the northern constellation of Coma Berenices, between Arcturus and Leo, and the South Galactic Pole is in the southern constellation of Sculptor, near Cetus and Fomalhaut.)

More Globes

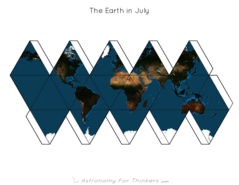
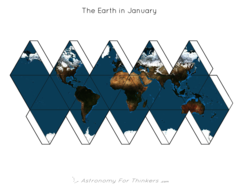
As long as we’re making paper globes, why not put different pictures on the globe? (After lots of frustrating debugging) my code is now fairly reliable, and it only takes a few button clicks and a different source image to make a different globe. How about the earth at night? How about comparing the appearance of the earth in January with the appearance of the earth in June? Most composite images of the earth are made by carefully putting together satellite pictures taken when there were no clouds, so you get a good view of the surface — what if we leave the clouds in the picture? Can we notice any interesting weather patterns? What about the moon? Here are some polyhedra made with some of these alternate source images, or at least ones I could find.

Just for fun, here are a couple of reminders that the earth is actually half in sunshine and half in darkness at any given time.

Observant people might notice a few interesting things in the globes given above. In the pictures with clouds, you can see a line of clouds running roughly around the equator. This is a fairly persistent weather phenomena and is partly responsible for all of the rain forests located along the equator. You might also notice the swirling patterns typical of the mid-latitudes. In the earth at night you can clearly see the earth's human population distribution from the lights of civilization. One thing you might notice is that the majority of the earth's population lives in the northern mid-latitudes. (The poles are too cold, the equator, at least in my opinion, is too hot and muggy, and the southern mid-latitudes contain mostly ocean.) I’d also like to mention that, regrettably, the source imagery that I use for the earth’s appearance does not include sea ice. If it isn't land, it’s blue in the pictures. This is the main reason you don't see much difference in Antarctica between January and July. We'd have a much more impressive view of the poles, I think, if we could see the Arctic and Antarctic oceans covered with white. If we compared the July and January pictures, we could also get an impression of the seasonal growth and shrinking of the polar sea ice.

The Earth, The Moon, and Mars to Scale

Since I have decent source imagery for the Moon and Mars, I really wanted to make a set of globes showing the Earth, the Moon, and Mars, all at their relative sizes, so you could set them side-by-side and see how they compare. If you could make three such scaled globes, what do you think they would look like? This is the set of icosahedra I came up with:

And here are the templates, if you want to make them yourself:

How far apart should you put them? If you want to take your paper globes for the earth and moon, and place them so that the distance is to scale with the sizes, how far apart should they be? And what about the sun? How big and how far would a model for the sun have to be?

There’s a fascinating story to be told about how the ancient Greeks figured out the sizes and distances of the Earth, the Moon, and the Sun. You can see the clues in the sky for yourself if you know where to look. (There's an abbreviated version of the story in my curriculum blueprint for astronomy.) But for the purposes of this discussion, I’m just going to give away the answers and tell you where to put the moon and sun. Nevertheless, I suggest pausing for a moment to see if you can estimate for yourself how far apart to put your moon and earth globes, and how large and how far to make the sun. The earth's globe is a little under 6 inches across, and the moon is about 1½ inches across.

* * *

If we take the “diameter” of the icosahedron as the distance from one point or vertex to the opposite vertex, then the diameters of the earth and moon given here are 5.7″ and 1.56″ respectively. (Mathematically, this is the diameter of the “circumscribed sphere,” i.e. the sphere touching all the vertices of the icosahedron.) If we take these diameters as equivalent to the diameters of the planetary spheres, and scale the distances to these diameters, then the moon and earth should be 14 feet plus a few inches apart. Unless you are in a large auditorium or something, you need to place them on opposite sides of the room. The sun would have to be nearly 52 feet across — maybe the size of your house — and it would have to be about 5600 feet away — over a mile, perhaps the distance from your house to the nearest Starbucks. If you do imagine such a sun somewhere, imagine the globe for Mars about a mile and a half from it — about 8500 feet.