The Sun, the Moon, and the Stars
(A Curriculum Blueprint)
What follows is an attempt to sketch out an interesting, logical story, by which you and your children can explore the skies over your heads, and discover what our neighborhood in space is like in a first-handed and active-minded way. This “blueprint” is somewhere between a bullet point outline and a full set of lesson plans, and it is meant to provide broad guidance while still allowing the flexibility to adapt to varying contexts and circumstances. (This flexibility is especially relevant in astronomy, as you will probably want to take advantage of different events in your sky as they happen.) It is my intention to offer a members-only “content library” at some point in the future, which will include some worksheets and slideshows and things, and will eventually include a full set of lesson plans.
The first three units of this curriculum “blueprint” are largely observational, and provide the evidence or the “clues” for later units. They attempt to familiarize the student with his or her own sky, and to gather and organize observations that anyone can make about the the sun, the moon, and the stars. The order of material in these three units is fairly flexible, and can be shuffled around to match the current events in your own sky. I recommend starting the constellations as early as possible. Begin by familiarizing yourself with the stars currently in the evening sky, and then continue to study new constellations as the seasons change. I recommend studying the face of the moon around the time of a full moon, and I recommend beginning a study of the phases of the moon just after a new moon, when the beautiful sliver of a crescent moon appears in the evenings over the sunset. (If there are any eclipses coming up, that is obviously a good time to discuss eclipses, although interpreting the clues provided by eclipses involves some abstract thinking skills.) The material in these basic units has been used quite successfully with children in the approximate age range of 8-12.
The last two units of this “blueprint” gather a few more important clues and then attempt to assemble the clues and put together all of the puzzle pieces that we have collected so far. In these units, we attempt to build up a scale model of what our neighborhood in space would look like if we could see it from the outside. These units involve some geometric reasoning and abstract thinking, and if I were teaching children at the younger end of the elementary range, I would omit the more challenging portions of the last two units, or perhaps omit these units completely, until the children were slightly older. With younger children, I would just have fun exploring the skies and discovering the patterns and the rhythms. For children with sufficient geometric reasoning skills, the five units together could make a fairly comprehensive (and fascinating, I hope) study of astronomy. I think they can provide each child with a sense of recognition of everything in the visible sky, and a personal grasp of his relationship to the world and the outer space around him.
A Few Stray Threads
There are a few topics that could be productively introduced in a variety of places, and/or built up in pieces as we go along. The organization in astronomy is somewhat flexible, and you can start with whatever interesting things are happening in the sky right now (full moon, pretty evening constellations, and so on). The following couple of topics should be kept in mind as we go along, and woven into our story at whatever point seems appropriate.
Cardinal Directions and the Compass Rose — Cardinal directions and the compass rose relate to the motion of everything in the sky, and discussion of these things could come at various times. Considering its fundamental importance, however, it should come very early in the story. If you start with the sun before the stars, you notice that the sun always rises at the same place on the horizon (or nearly so), and it always sets at the same place (or nearly so), and you name those directions "East" and "West." If you start with stars, you can notice that the same stars are always present on the same side of the sky (on the northern side, if you live in the Northern Hemisphere), and you notice that there is one in particular star that is always in the same place. The North Star marks North. And after you've discovered that certain things in the sky are always in the same directions, and you have named the four cardinal directions, then you ask the question of how to systematically name names for every direction on the horizon. If you want a coloring activity, you can color in a compass rose.
Is the Earth Round? — What happens if you drive or sail towards the horizon? Will you ever come to an edge? Can you fall off? The fact that the Earth is round is "common knowledge" in the modern civilized world, but I think it is still valuable to step back at some point and ask how we can be sure for ourselves that this is true. The Ancient Greeks figured it out more than 2000 years before space travel was invented, and more than 1500 years before the telescope was invented, and they only needed clues that you and I can see in our own lives. (Not only were they able to figure out that the world is round, they were even able to estimate the circumference. And they didn't even have a complete map of the surface. Their "world map" covered less than half of the Northern Hemisphere, and the rest was a total mystery. Imagine knowing that you live on a sphere, but not knowing what's on the other side!) So what are the clues? How can we see for ourselves that the Earth is round? The clues come from several places, and we'll discover them as we go along.
The Map of Outer Space
The Major Constellations
If you live in the country, you can see a beautiful night sky, rich with stars. If you live in a city, you won't be able to see nearly as many stars, but you should still be able to see the brightest stars when the skies are clear and when you are not too close to a bright shopping area or commercial district. So let's at least learn the bright “landmarks” in outer space, and then you can go hunting for the dimmer details the next time you go out of the city. To help learn the “geography of the sky,” you can study the maps in an atlas of constellations, or if you want to draw your own maps you can use these constellation worksheets. (There are also many apps for mobile devices, of varying quality, that can show you which constellations you are currently looking at. Stellarium makes one of the better ones.)
The Northern (Or Southern) Wheel — If you live in the Northern Hemisphere, you will find that there is a group of constellations that are always there, as permanent decorations in the northern sky, like faithful familiar friends. If you learn to recognize these constellations, you can always tell which way is north at night. There is the Big Dipper (as it is known in the United States), and Queen Cassiopeia, plus some other dim things you can go hunting for in darker skies, like the Dragon and Cassiopeia's husband. How is it that the constellations in the north can stay the same, when all other constellations are in different places at different times? If you pay close attention for several hours (or make a star trail photograph), you will discover that the northern stars just turn in counterclockwise circles, like they are all on a wheel spinning forever in the northern sky. And the North Star is right in the middle, like the pin in a pinwheel. This is why it stays forever in the same place in the sky while all of the other stars change positions. If you live in the Southern Hemisphere, you can't see these northern stars, but you can see a different set of stars forever turning clockwise on a wheel in the southern sky.
Scorpius and Sagittarius — This is a big, beautiful group of some of the brightest stars in the sky, but they aren't very well known in the Northern Hemisphere. For Northern Hemisphere viewers, the stars in the northern sky are always up, but the stars in the southern sky, including Scorpius and Sagittarius, are rarely up. If you live too far to the north (in Canada or in most of Europe), you can't even see them at all. (On the other hand, if you live in the Southern Hemisphere you get to see them most of the time.) This part of the sky has an especially bright and beautiful patch of the Milky Way, and it is a good place to go hunting for beautiful things in a telescope. This is also where you will sometimes see trespassers — stars that slowly wander around and don't have a constellation of their own to belong to. We can call these “wandering stars,” or we can borrow the Greek word for “wanderer” and call them “planets.”
The Summer Triangle — This is a trio of three of the brightest stars in the sky, forming an elongated triangle. If you think of the triangle as being like an arrowhead, it points south, so this is another way that you can tell directions from stars. In the northern hemisphere, this patch of stars is not always up, but it is “often up,” so it is a useful group to know. (Technically, in modern star guides, this triangle is an “asterism” and not a “true” constellation.) Each of the three corners of the triangle has a more complex constellation of its own to help you recognize it, and there are also some pretty but dim things to hunt for. There is a cute Dolphin, which is made entirely of dim stars, but there are so many so close together that sometimes you can even see the Dolphin in a city. There are also a few hidden treasures you can go hunting for with a telescope.
Orion and the Winter Hexagon — Orion might be the most well-known constellation in the Northern Hemisphere. He isn't up as much as the Big Dipper, but he is brighter. He is also surrounded by a huge raft of bright constellations nearby. (This is probably one of the two brightest patches of the night sky, at least the sky that you can see from the United States. Scorpius and Sagittarius form the other.) There are a couple of closely-knit star “families” or “clusters” here. There is a red V-shaped group forming the horns of Taurus, and a smaller blue group close by. Both of these “star clusters” are gorgeous in binoculars. This is also another part of the sky where you can sometimes find planets.
Leo the Lion — In the evenings of spring, much of the sky is fairly dark, but there is one bright and distinctive constellation in the middle of the ocean of darkness. This is Leo the Lion, and he is a useful connecting figure in the globe of stars. He lies roughly in the center of the “Arc to Arcturus,” and roughly halfway between the Hexagon of winter and Scorpius & Sagittarius, which are visible in summer. (The Milky Way is far away from this part of the sky and there aren't many treasures here to hunt for ... unless you have a very powerful telescope, in which case this is a great place to hunt for distant galaxies.)
The Andromeda Story — In many parts of the sky the constellations are a bit jumbled. There are individuals scattered around, with only a thin relationship to each other if any. But the skies of autumn evenings contain a whole group of constellations, all characters from the same story, all together in the sky. This is the classic tale of Andromeda and Perseus. [There were a couple of versions of this story written in the classical world, and a couple of movie versions made in the modern world under the name “Clash of the Titans.” It would be fun to tell or watch at least one version of the story before or along with studying these constellations. I would usually just tell my own brief 5-minute version of the story to my students before discussing the constellations.] The princess Andromeda, her parents Cassiopeia and Cepheus, the hero Perseus and his winged horse Pegasus, even the sea monster Cetus — they all have their own constellation in this part of the sky. (We've already met Cassiopeia and Cepheus. Now we can find the rest.) If we pay close attention, we can also find a couple of weird stars in this part of the sky. Most stars are always the same — the same color, the same brightness, the same place in the sky. They are eternal. But there is one that, if we pay close attention, we can see it wink! This “Demon Star” turns off for a few hours every few days. There is also another star in Cetus that sometimes isn't there. If we pay attention for a long time, we find that it gradually turns off and on roughly once a year. And this is another part of the sky where we sometimes find planets, although they don't go through any bright constellations here.
The Celestial Sphere
A Globe for Stars — As we were discussing all of the constellations and making our maps, you may have wondered … How do they go together? Can we assemble all of the constellations into one single map of everything? Well, if we could put all of the maps together, what shape would the entire map have to be? It would have to be a sphere, or a globe. Our map of the outer space around us has to take the shape of a sphere, showing us what is around us in every direction. It will be just like a globe of the Earth, except we look at it from the inside instead of the outside. (We can't really make a huge globe and stand inside, so we usually make a normal globe and look at it from the outside, but we turn all of the constellations inside-out so they look right when we look at them from the outside.) If we want, we can buy a “celestial globe”, or we can make one out of paper.
Planispheres — The globe is nice to have, but it isn't very convenient to carry around. It is also hard to figure out which half is up in the sky and which half is hidden by the horizon at any given time. What if we want a more convenient flat version of the globe, like a flat world map? One thing we can do is to flatten the celestial sphere in a special way. We can cut it into two hemispheres — the “Northern Hemisphere of Stars” and the “Southern Hemisphere of Stars” — we can press them both flat into disks, and then we can glue the two disks back-to-back. We'll have a complete “world map of stars” in the shape of a double-sided disk. We call this “sphere in the shape of a plane” a “planisphere.” And now that it is flat, we can make a cover to hide half of the stars, and reveal the other half, and it can show us which half is up and which half is down. And we can turn or rotate the disk to show us the sky at different times of the day. If we do this, we will have made a rotatable map that can show us which constellations are up at any time we want. We can easily buy one, or we can make one out of paper. [I thought that my paper planisphere was generally pretty successful in my classroom, but the one thing that my students always complained about was the difficulty in cutting out the windows and the other round shapes. So I also made a polygonal version that is easier to cut out, but it doesn't rotate smoothly.]
Seasons, Latitudes, and Sundials
Looking At the Sun
Risks and Rewards of Looking at the Sun — One of the best ways to learn about something is to look at it, but isn't looking at the sun dangerous? Sometimes people do damage their eyes by looking at the sun, but most of the time it happens because they did something reckless, like ignoring the pain and staring at the sun even when it hurts, or by looking at the sun through something. A quick glance with a healthy eye on an ordinary day is fine. Just don't do anything that hurts, and be careful if the circumstances are unusual in any way. Also, do you suppose it makes a difference whether the sun is high in the sky or close to the horizon? When you feel the warmth of the sunshine on your face, is it warmer when the sun is high in the sky, or low? The sunshine is much more powerful when the sun is high in the sky than when it is close to the horizon. When the sun is high in the sky it hurts a little to look at it, but when it is rising or setting you can go ahead and enjoy the beauty all you want and it won't hurt your eyes. And maybe you'll even learn something.
Ways to Get a Better Look — Even when it is safe to look at the sun, it is hard to discover anything interesting. Whenever we look at the sun, it is usually buried in a puddle of glare. We seldom get a clear view of the sun itself as a physical object. Sunglasses don't help. (And looking at the sun through sunglasses can actually be risky, because they might block the harmless portion of the color spectrum, while still allowing the most harmful rays through. This is an example of the risks of looking at the sun through something.) However, there are “super-sunglasses” that are made especially for looking at the sun. They're called “eclipse glasses” and they're made for watching solar eclipses, but they work just as well for looking at the sun on a normal day. Binoculars and telescopes can sometimes give us a better look at far away things, but looking at the sun through binoculars and telescopes is a very bad idea — unless you do it in a special way. Sometimes you can buy “super sunglasses” or “solar filters” made especially for your telescope or binoculars. You can also use a very simple projection method: Instead of looking through binoculars or a telescope directly, you can put a card or a screen where your eye would normally be, but farther away, and then by adjusting the distance you can make an image of the sun appear on the card.
Some Simple Observations — What color is the sun? And don't automatically say yellow. Actually look at the sun, or look at sparkles of reflected sunlight in water or glass or metal. The sun is colorful when it is low in the sky, but when it is very high in the sky, it is pretty close to white. Not only is the sun more powerful when it is high in the sky, its light is more “pure” and less colorful. The “pure” sunlight lights up the world with “white light”. What shape is the sun? If we can see it without the glare, with eclipse glasses or maybe through thin clouds, we see it's a perfect, beautiful, glowing circle. (If you look at it — carefully! — with telescopes or binoculars, you might see a few spots on the sun, but otherwise it looks like a perfect heavenly circle.) So the sun itself is probably a sphere? If you study how the sun looks in the sky, you might also notice that the sky around the sun is brighter than the sky farther away, like a halo. We call this the “aureole.” Do you suppose the aureole is actually part of the sun, like an atmosphere, or just the glare of sunshine coming through the air above you?
Tracking the Sun Across the Sky
If you search the internet for ways to make a simple homemade sundial, you will probably find many people telling you to draw a clock face on a paper plate, push a pencil through the middle, and place it in the sunshine. The shadow of the pencil is supposed to turn around the center like the hand of a clock, and thus show you the time. Let's think about this. Let's do some “thinking practice.” How would the sun have to move through the sky to make the shadow of the pencil sweep around in a circle like the hand of a clock? Does the sun actually do that? If it doesn't do that, what does it do? How could we figure out what the path of the sun across the sky actually looks like?
Tracking the Sun — Wouldn't it be fun if we could reach up with a giant marker and draw on the sky? That would make tracking the sun very easy. If we can't do that, what could we do? Maybe we could put stones around us to mark the direction of sunrise and sunset? That's what some stone-age people did. Maybe we could track shadows? Instead of drawing the trail of the sun across the sky, we could draw the trail of shadows across the ground. Maybe we could make a bowl, and put something in the middle to cast a shadow, and then the bowl would be like an upside-down sky and the shadow would move across it just like the sun moves across the sky. Or we could also just try to track the shadow of a vertical stick or post. It would be like the paper-plate sundial, but without the marks. We'd be finding out for ourselves how shadows move across the ground. Another thing we could do in the modern world is to use time-lapse photography to record the sun moving across the sky. So let's try one or all of these things and see what we discover.
Sunrise and Sunset — The sun always rises every day, but it doesn't rise just anywhere. It always crosses the horizon at the same place. [This assumes that you don't live near the poles, and that you have only been watching for a short time. If you pay attention long enough, you discover that the sun doesn't rise exactly in the same place all the time, but instead it oscillates each year around a central place on the horizon.] This special direction is named east. Does the sun rise straight up? No, it rises at an angle. [It tilts to the right, if you live in the Northern Hemisphere.] In the same way, the sun always sets in the same direction, at the same place on the horizon. We call that direction “west.” It also does not set straight down, but instead crosses the horizon at an angle.
The Sun at Noon — Where is the sun at noon? Overhead? If it were really and truly straight overhead (or more technically at the “zenith”), what would happen to your shadow, or to the shadows of vertical poles? Does that ever happen? There is a special time of day when the shadow is shortest, and it points due “north” at that moment, but the shadow never disappears completely. [Again, this assumes that you live in the Northern Hemisphere. If you live near the Equator, the sun does touch the zenith sometimes, and if you live in the Southern Hemisphere, shadows point south at noon.] This is the special marker of the day that we call “noon,” and our whole way of counting time of day starts from that moment.
The Solar Wheel — So we could describe the path of the sun across the sky as an arc from east to west, tilted towards the south. [If you live in the Southern Hemisphere, it will be tilted towards the north, and if you live at the Equator it will pass overhead.] Where does the sun go when it is down? Early cultures had lots of fun stories about gods or mythical beasts devouring it or carrying it below ground somehow. If we use our imagination to picture the sun's arc across the sky as a portion of a circle, then when the sun is down it is just moving along the rest of the circle. The sun appears to turn around us in a circle once a day, but only part of the circle is above the horizon, and the rest is below the horizon. This is what gives us day and night. (One explanation might be that the sun is “orbiting” around us in circles. Another might be that the Earth is round, and it spins, and it is really us that are turning in circles while the sun stands still. If that is so, then we have daytime when our side of the Earth is facing towards the sun, and we have night when our side of the Earth is facing away from the sun. Either way, this daily circular motion is what gives us day and night, and if we want to measure time of day in a mathematical way we will need to do it by cutting this circle into pieces.)
The Seasons and the Solar Wheel — So it looks as if the sun is going around us in circles, but the circles are tilted, and they are partly below the horizon. What if we watch the sun every day for a long time? Will the path ever change? How might it change? If we do watch for a year, we discover that the sun's path across the sky is always a tilted arc [unless we live near the Equator]. The tilt never changes. But the arc rises higher in summer, and sinks lower in winter. [To throw in some modern technical jargon, the tilt of the apparent arc in your sky depends on, and is equal to, your latitude on Earth. The northerliness or southerliness of the circle depends on the sun's position along the ecliptic, and it is measured by the sun's “latitude” or “declination” on the celestial sphere, which oscillates annually between the two limits.] In summer, more of the circle is above the horizon and less of the circle is below the horizon, so the days are longer and the nights are shorter. In winter, more of the circle is below the horizon, and less is above, so the days are shorter and the nights are longer. When is the sun most powerful? When it is high in the sky or low? In the summer, we have more hours of more intense sunshine, and in the winter we have fewer hours of less intense sunshine. What is this going to do to the world and the weather? If we want to name special moments in time to mark the passage of the seasons, we can use the two moments when the sun reaches the most northerly and southerly extremes. At these moments, the sun seems to stop moving north or south, and it seems to “stand still” before it turns around and heads back in the other direction. So we call these two special days of the year the “stations of the sun” or the “sol-stices.” We can also name the two days in spring and fall when the circle is exactly in the middle. On these days, the sun rises due east, sets due west, and the circle is exactly half up and half down, so the days and the nights are equal. We can call these the “days of equal night” or “equi-noxes.”
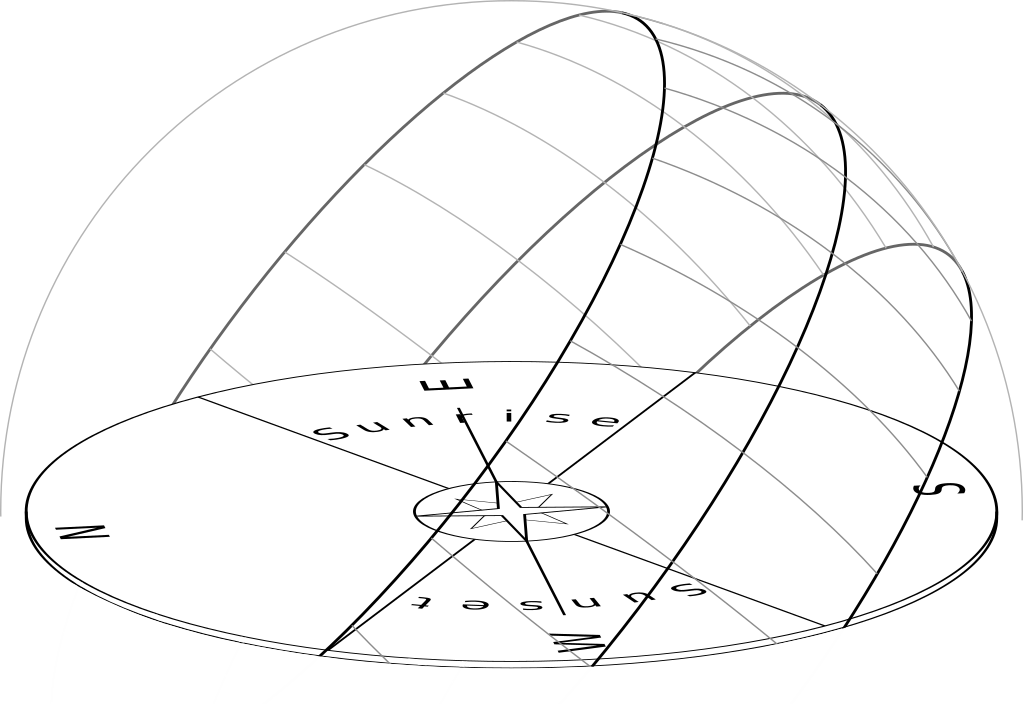
Do you see why early cultures so often made the sun into a god? Do you see how it controls the day and the year and drives the rhythms of all life on Earth?
A Model of the Sky-Dome — Stone-age people would often place stones or cut windows in walls to mark the position of sunrise on the solstices. This way, they could compare the sunrise to the markers every day, and see how much longer it would be until summer or winter. Nowadays, astronomers call these marking devices “horizon calendars.” Later, kings and emperors would sometimes have their astronomers build fancier versions of the same thing, and they would make royal observatories. You could do something similar in your back yard. Or you could make your own paper solarium to record everything we've discovered so far, and to make a model of the sun's wheel or the “solar highway” across your sky.
The Climates of the Earth
The Sun in Different Parts of the World — So far we have done a pretty thorough job of tracking the sun where we live. But is it the same everywhere? Maybe you've heard that the seasons are backwards in the Southern Hemisphere. Maybe you've heard about the “Land of the Midnight Sun.” Let's take a quick tour of the world, and see what the sun is like in the skies of different parts of the world. And we discover: If you travel east or west, it makes no difference. (Except you might have to adjust your clocks if you travel far enough.) The “solar highway” across the sky is the same as yours for everybody to your east and your west. But traveling north or south makes a big difference. There is always a “highway” across the sky from east to west, but it is tilted at different angles in the sky. The farther north you go, the more it tilts to the south, and vice versa. (Why do you suppose that would be? Here we have another clue that the Earth is round. Traveling over a curved surface makes us see things in outer space from different angles.) If you could go to the poles, the circles would be horizontal, and at the Equator, they stand straight up. For most of us, they are more or less tilted depending on how far we are from the Equator. (So the simple “clock face” sundial would really work at the poles … or at least it would work at the North Pole. At the South Pole, it would run backwards.) In the Southern Hemisphere, the southerly December circle is the higher one, and the northerly June circle is the lower one, which explains why the seasons are reversed. At the Equator, the sun's circle is always half up and half down, and the sun goes near to the zenith every day of the year. At the Equator, there is no “longest day of the year” or “shortest day,” and they don't really have seasons in the same way as people elsewhere.
The Climates of the Earth — The Ancient Greeks realized that the Earth must be round, even though they only had a map for a small part of it. They had no idea what was on the other side of the sphere. But they at least realized that it could be divided into “zones,” layered from north to south. (They also managed to estimate how large the sphere is, but we'll talk about that later.) Far to the north, there was the inhospitable “Arctic Zone,” and there was probably a mirror-image “Anti-arctic” zone at the opposite pole. Running around the middle or the “waist” was an inhospitably hot zone. (The Greeks had the Saharan and Arabian Deserts to their south, and to them the entire “torrid” zone running around the Earth's middle was presumably hot barren desert. They didn't know about tropical rain forests. Also, our word “climate,” like our word “inclination,” comes from a Greek word meaning “slope” or “zone.”) This left two comfortable “inhabitable” zones sandwiched in between the hot equatorial zone and the two cold polar zones. What kinds of creatures or people lived in the southern inhabitable zone? The Ancient Greeks had no idea. If you look at a modern map of the climates and the biomes of the Earth, you can still see a basic layered pattern, underneath all the jumble caused by coastlines and land masses.
Latitude Measurement — So how far north or south you live can make a big difference on your weather and your way of life. Is there a way to measure “how high” you are on the Earth? One way would be by the length of your longest day. If you live in the “Land of the Midnight Sun,” your longest day is 24 hours. If you live near the Equator, your longest day is barely more than 12 hours. So it might be useful to name “how high” you are, to measure how far you are from the Equator, by how long your longest day is. At least one Ancient Greek astronomer did it that way. In the modern world, we measure your “latitude” as the number of degrees of a circle you are from the Equator. At the Equator, you have a latitude of zero, at the Poles you have a latitude of 90, and most of us who live in the “northerly mid-latitudes” have a latitude of 30-50 degrees or so. While we were exploring how the sun moves across the sky in different parts of the world, you may have noticed certain special latitudes on Earth. There are two special boundaries near the Equator, separating the Equatorial region where the sun can sometimes go straight overhead from the mid-latitudes where the sun can never go straight overhead. We call these two special dividing lines the “Tropic of Cancer” and the “Tropic of Capricorn”, and they have a latitude of about 23.4 degrees north or south. (The names come from constellations, but that's a long story. For now, you can just notice that if you live at these latitudes, then those constellations pass nearly overhead.) There are also two special circles near the poles. Inside these circles there are some days in winter when the sun never rises, and some days in summer when it never sets. Outside these circles, the sun always rises and sets every day of the year. We call these two boundary circles the “Arctic Circle” and the “Antarctic Circle”, and they have a latitude of about 90 - 23.4 or 66.6 degrees north and south. If you want to, you can think of these four special circles as the boundaries between the “inhabitable” and “uninhabitable” zones of the Ancient Greeks.
So not only is the sun the ruler of the daily and annual rhythms of life on Earth, it also controls the distribution of weather and of life on Earth. The sun not only gives us day and night and summer and winter, it also gives us the different “inclinations” or climate zones of the Earth.
The Beautiful World of Sundials
So let's come back to the question of how to make a sundial. If you want to make a geometry-based sundial, one that recognizes and monitors the motion of the sun in your sky, you need to make the shape of your sundial match somehow the shape of the sun's path in your sky. You need to take into account both your location on Earth, and the season of the year. But there are many ways you could do this, and there are many beautiful designs of sundial that you could make, both simple and complex.
Sundials With Calendars — I would say that there have been two periods in Western History in which sundials and sundial-makers flourished: the classical world of the Ancient Greeks and Romans, and the “Golden Age of Sundials,” corresponding roughly to the Renaissance and the Enlightenment in European history. Before the Greeks, most early agricultural societies noticed that shadows are longer in the morning and evening, and shorter in the middle of the day, and they used this fact to help them know when to do certain things each day. (Perhaps they came in from the fields for lunch when their shadows were shorter than they were, or something like that.) And sometimes they would even make little devices with marks on them to help them, like the simple “sundials” invented by the Egyptians and Babylonians. (A simple paper plate “clock face” sundial would be like this.) But it was the Greeks who first applied geometry, recorded the path of the sun in the sky as a circle, and divided the day into equal slices of time by dividing the circle into equal slices. It was also the Greeks who first realized that each sundial had to be tilted or otherwise adapted to each city's latitude, because the sun's arc in the sky is tilted differently in different cities, and that sundials need different curves if they are to track the sun in different seasons. These masters of geometry and of stone-carving made sun-tracking sundials in the shape of spheres, cones, and cylinders, as well as flat horizontal plates, and created the first scientific instruments in human history. All of the Greek sundials used a metal needle or something similar to cast the shadow of a point onto a grid, and you could read both the time and the season by where the point fell on the grid. If you'd like to make a Greek Sundial of your own, you can make a paper hemispherical sundial, or a “gnomonic” or “butterfly” sundial.
Sundials Without Calendars — Many centuries later, during the “Golden Age of Sundials,” people already knew well how the sun moves through the sky, but they were starting to travel more and have meetings more often. They needed simple, practical time-telling devices more than they needed “sun-tracking” scientific instruments. So they invented simpler, easier to read sundials that ignored the calendar and simply told the time of day. (Clocks had actually been invented by this time, but they were still huge and unreliable. Sometimes towns would have a town clock in a tower somewhere, but they would still need to use sundials to reset the clock to the correct time every day.) But how can you ignore the calendar, and still make sure your sundial works correctly in every season? The key difference in these sundials is to use an edge to cast a shadow instead of a point or tip of some kind, and to make sure that the stick or the edge that you are using to cast the shadow is not vertical, but is tilted so that it is parallel to the axis of the sun's wheel. The sun's “wheel” has to appear to turn around your edge or stick like an axle. (Or if it is really the Earth that is spinning, then the stick or the edge of your sundial will need to be parallel to the axis of the Earth. In a correctly-made sundial, you should be able to see the axis of the Earth reflected in the tilted gnomon of the sundial.) Using an edge makes the sundial much easier for a casual user to read, and making sure that the edge is tilted and lined up with the axis means you don't have to worry about the seasons. It will keep regular time regardless of the season. It was during this era that most familiar “garden variety” sundials appeared, and these are the ones that most people think of today when you say “sundial.” If you want to make your own, you can try one of these simple paper sundials, or this paper cube sundial, and you can find many more designs by searching the internet.
Clocks and Calendars
Modern Clocks and Horology — Why are there 24 hours in a day? Nature gives us the day and the year, but there is nothing in nature that lasts exactly an hour. It's a completely made-up unit of time. Where does it come from? We simply decided to cut the day into equal pieces and count the pieces. An hour is a fraction of a day. (The art of dividing a day into useful counting pieces used to be called “horology.” And it wasn't possible before the Greeks realized that you can view the cycle as a circle, and figured out how to make regular geometric “rulers” that could cut the circle into evenly-spaced pieces.) But why did we choose to cut the day into 24 pieces? Why not 17, or 35? Do you notice anything about the numbers 12 and 24 that might make them better numbers to use than 17 or 35? They have many factors. You can divide them in many ways — into halves, thirds, quarters, and sixths. There are 24 hours in a day, because 24 is a highly divisible number. (This is also why there are 60 minutes in an hour, and 60 seconds in a minute. Try listing all the factors of 60.)
Sundial Time vs. Clock Time — Why don't sundials and clocks agree? Daylight Savings Time is one reason. We make the clocks different from sundials by one hour, on purpose, for part of the year. Maybe you can see another reason if you think carefully about time zones. Why do we have “time zones,” and why are they designed the way they are? We want everybody in the same area to be able to use the same clocks, and have everybody agree on what time it is. But is the sun in exactly the same part of the sky for everybody? The “sun time” is a few minutes later for people 100 miles to your east, and a few minutes earlier for people 100 miles to your west. So when we made everybody in the same area use the same clock time, we made it so that their clocks couldn't always exactly agree with their sundials. We set up the shapes of the time zones (thin slices running north-and-south, with clock-time equal to sun-time in the middle of each zone) to minimize this problem, but we can't get rid of it completely. There is also another weird reason sundials don't agree with clocks. When our technology was finally good enough so that we could make clocks that kept time accurately to within a few seconds for months or years at a time, we discovered that the sun itself doesn't keep perfect time. It speeds up and slows down a little bit as the months go by. After a year it comes back to where it started, but the sun can be as much as 12 or 14 minutes fast or slow in certain months of the year. If we were only using sundials to tell time, we'd never know the difference. But if we want to use a super-precise modern clock system to tell time, this means that our sundials will sometimes be a little “fast” or “slow” compared to our clocks, not because the clocks are wrong, but because the sun is wrong. So if you ever visit or study a very precise, modern sundial, you will probably find two things nearby to allow you to tell clock time from the sundial: a constant longitude correction based on how far you are from the middle of your time zone, and a calendar showing you how fast or slow the sun is today. (The “sun speed” correction is usually called the “Equation of Time.” The calendar may look a little like the figure-8 “analemma” that you sometimes see on globes, and it represents the same thing.)
Modern Calendars — Early agricultural societies needed a way to know when to plant and when to harvest. You can't just say “It feels like spring, so I think I'll start planting today.” You need more precise timing signals than that. So farmers learned to recognize certain patterns in the world around them. Then they could use these events as rough “year-markers” — the annual flooding of the Nile, for example, or perhaps the blooming of the bluebells or something like that. But what if we need a more mathematical and precise way of counting days and naming different parts of the year? Where did our modern calendar system come from? Counting moons is a good way to measure the passage of large amounts of time, but unfortunately there isn't an even number of moons in a year. So we can't count moons and count years at the same time, and have the two counts line up. So we'll cut the year into twelve “months,” and each of them will be close to one “moon” but not exactly, and we'll have to fiddle with the exact lengths to get the counts to come out right. Our modern 12-month system is called the “Gregorian Calendar,” and the Gregorian Calendar is basically the “Julian Calendar” with a little tweaking. Julius Caesar realized that the Roman Empire needed a good, reliable calendar, so he told his astronomer to develop one, and this astronomer came up with more or less the system that we use today. (This is also why one of the months is named “July.”) Originally it started out with the solstices and equinoxes being a little like our modern “New Year.” Each event marked an important change in the seasons, and the beginning of a new month. If you were to design a mathematical, scientific calendar from scratch, that would be the most sensible way to do things. But in the millennia since then, the seasons have drifted a little through the calendar. Now the solstices and equinoxes happen about two-thirds of the way through their respective months, and hardly anybody notices them when they happen. Why do we use the four days to mark the beginnings of their respective seasons, instead of the middles? For the same reason that the warmest hours of the day are usually in the midafternoon. The sun makes the day warmer than the night, and the summer warmer than the winter, but not instantly. The world takes a little while to warm up and cool off. Maybe you have also noticed that the names of the months are not right. SEPTember, OCTober, NOVember, and DECember are not the 7th, 8th, 9th, and 10th months. They used to be, before the last two months were added to the calendar. Where do the names of the days of the week come from? That's another interesting story.
The Moon
The Face of the Moon
The Freckles of the Moon — When we look at the sun in the sky, we see a perfect glowing circle. It is truly a heavenly body. The moon is different. It has freckles and blotches. It has a face. (It is almost as if the moon is another world, with a landscape of its own.) Can we learn anything interesting by studying these features in the face of the moon? Do they ever change? If we examine the moon for ourselves, or study photos of it, we discover that it always has the same face. The freckles never change. They might be tilted one way or another depending on where it is in the sky, and we might not be able to see all of the freckles when the moon is not full, but we never see any new or different features. Isn't that weird? If the moon is a sphere floating loose in space, wouldn't we expect it to turn, and to show us different sides at different times? But it doesn't. However the moon is moving around out there in outer space, it is careful to keep one side always facing towards us, and to keep the back side forever hidden from us.
The Arrow Through the Moon — If we want to make a map of the face of the moon, how do we know which way to turn the map? We can't name the “top” side of the moon or the “bottom” side, because the face is tilted in different ways at different times. (And if you live in the Southern Hemisphere, or you look at pictures of the moon taken in the Southern Hemisphere, you can see that the face appears upside-down compared to how it appears in the Northern Hemisphere.) So how do we know which side is the “top” and “bottom” of the moon if it doesn't even have a top and a bottom? Notice that when we say that the moon is tilted, we are comparing it to our horizon. But if we compare the moon to the other things in outer space, and to the direction it is traveling in the sky, we discover that the moon is always turned the same way. We see that one side of the face is always pointing “forward” in the direction it is traveling through the sky, and one side is pointing backward. It is as if the face has an arrow through it, showing which way it is moving, from east to west through the sky. And once we have recognized the face, then we can also imagine this arrow, and find east and west. (So this is yet another way that we can tell directions if we are lost, by knowing the sky.) And perpendicular to this “arrow” is another arrow, which always points at the North Star. The moon does indeed have a “top” and “bottom” after all, we just have to stop comparing it to the ground and the horizon, and start comparing it to the sky and to other things in outer space.
What Galileo Saw — [Galileo may not have invented the telescope per se, but he was the first person to point one into outer space, and he discovered some fantastic and wonderful things that nobody else in history had ever seen before: the phases of Venus, the moons of Jupiter, blemishes on the sun, the stunning richness of stars in the Milky Way, and the existence of mountains and plains on the surface of the moon. (He wrote about these things in Sidereus Nuncius, which is fairly light reading in translation and is fun to read to students.) And these discoveries helped to radically change our awareness of what things are like in outer space. Considering this, it may be worth saving this discussion until later, outside of a narrower discussion of the moon. On the other hand, as long as we are getting to know the moon, it might be interesting to briefly discuss the invention of the telescope, and the mountains and the “seas” that you can see with your own telescope, or maybe even a good pair of binoculars. If you do it this way, this would also be a good time to give students their own detailed map of the moon. Furthermore, there's nothing wrong with reminding or repeating information sometimes, so perhaps the best approach is to briefly introduce or foreshadow Galileo and the telescope here, then come back to the subject and give it a fuller treatment later.]
The Phases of the Moon
You have probably already seen the moon in different shapes, and maybe you even know some of the names for some of the shapes. But you probably haven't paid much attention to where each phase is in the sky, or to what time of day it is when you see it. So let's briefly review the names of the phases, and then we'll do a more careful and systematic study of the rhythm of the phases, and what we can learn from it.
The Repeating Cycle
Did you notice that beautiful, thin sliver of a crescent moon decorating the sunset last night? [I recommend starting a study of the phases of the moon just after a new moon, when the waxing crescent appears over the sunsets.] Let's see if it is still there tonight, and tomorrow night, and if it is there, then maybe we can watch how it changes day by day. Maybe we can even keep a journal.
The Evening Moons — If we watch each evening, we will see the moon creep a little higher over the sunset each day, and grow a little larger. After about a week, it will be a semicircle, or a “quarter moon,” and it won't be over the sunset anymore, but it will be a quarter-turn away from the sun. After another week, the moon will have crossed all the way across the sky, and it will have grown all the way into a full moon. Now it is a full moon in the opposite place as the sun, rising in the east just as the sun sets in the west. What will happen if we keep watching in the evenings? We won't be able to find the moon in the sky anymore ... unless we get up before dawn, and start looking in the mornings instead of the evenings.
The Morning Moons — If we were to get up on any given morning and go out to enjoy the sunrise, we might see the moon or we might not. If we start watching in the morning at the same time that we stop watching in the evenings, i.e. when the moon is full, then we will see the moon setting in the west just as the sun rises in the east. Now if we keep watching each morning, we will see the moon gradually creep closer and closer to the sunrise each day, growing smaller and smaller. After about a week, it will be a quarter-moon, and it will be about a quarter-turn away from the sun in the sky. After a few more days, it will be a beautiful crescent moon over the sunrise, and a few days after that it will disappear into the sunrise. (Where do you suppose we need to start watching for it after that?)
The Monthly Cycle of Phases — The phases go in order, over and over again, in a repeating cycle. And each phase has its own place in the sky and its own time of day when you can see it. The full moon is like the “opposite moon.” The full moon only happens when the moon is on the opposite side of the sky from the sun. We can think of the crescent moon as the “sunrise” or “sunset” moon. We only see it in the evening over sunsets, or in the morning over sunrises. (Sometimes if we look hard enough, we can see it in the daytime sky, not too far away from the sun. But that's a challenge.) All of the phases that you can see in the evening are the “growing up” or “waxing” phases. All of the phases that you can see in the morning are the “shrinking” or “waning” phases. And so on.
Reasoning With Phases — If you see a crescent moon over the sunset, how long will it be until there is a full moon? If you see a quarter moon at the time of sunset, which way are you facing? If you see a full moon setting, what time is it? If you know how the phase cycle works, you can figure out all kinds of things when you see the moon in the sky. (Or you can figure out when and where you need to look for it, if you want to hunt for it.) To summarize the entire phase cycle in a little “model” we can make a lunar phase dial, and we can use this “phase calculator” to answer all kinds of questions.
Why Does the Moon Have Phases? — Sometimes people think that the moon has phases because the Earth's shadow is falling on it. In a way, this makes sense. The moon can't be glowing under its own power, like the sun, because then we'd see a full glowing circle all the time. So the moon must be glowing in the sunshine, and if the moon isn't entirely lit up, then it must be in a shadow of some kind. But let's use this as an opportunity for some more “thinking practice.” Let's look at the clues. For something to fall into Earth's shadow, where would it have to be in the sky? It would have to be on the far side of us from the sun, wouldn't it? Where is the moon when it has phases? It is not on the far side of the sky from the sun. Actually, the darkest phases are the ones we see when the moon is closest to the sun in the sky. So it can't be the Earth's shadow. You've probably noticed another clue if you've been paying attention to phases for any time at all: The bright side is always facing towards the sun in the sky, and the dark side is always facing away from the sun. It's as if the invisible part of the moon is simply the part of the moon facing away from the sunshine in space, and we could see it if only it were lit up by something else. It might seem a little odd, because normally we can still see the dark side of objects in sunshine, they are just darker than the illuminated side. But this may be because when things are in shadows here on Earth, there is usually still some “ambient light” from other things nearby that are in the sunshine. Maybe the dark side of the moon is so completely invisible in the sky simply because it is facing away from the sunshine, and there is nothing else nearby to give it any ambient light. (Actually, perhaps you've noticed that sometimes we can see the dark side of the moon, as if there is some ambient light nearby. When does this happen? Does this contradict or reinforce our theory?)
Hypothetical Phases — Sometimes it can be fun and interesting to play “What if?” Let's imagine for a moment how the Sun, the Earth, and the Moon might be arranged in space, and ask what kind of phases we would see in different circumstances. What if the moon were farther away than the sun? Could we ever see crescent moons or new moons? What if the sun were farther away than the moon, but only a little farther? We would see a complete cycle of phases, but the moon would rush through the “small” phases, and spend most of its time in the gibbous phases. When we saw a quarter-moon, we would see it fairly close to the sun in the sky. What if the sun were very, very much farther away than the moon? We would see very regular and evenly-spaced phases, and we would see quarter-moons almost a quarter-turn from the sun in the sky. Which of these situations do we actually see? What does this tell you about how far away the sun is? (If you can handle a protractor and a little work with triangles, you might even be able to measure the angle between the sun and a quarter-moon in the sky, and estimate how many times farther away the sun is than the moon. The Ancient Greeks tried this, and discovered that the sun and the quarter moon are so close to a right angle in the sky, that they couldn't measure the difference. So they reasoned that if the difference were more than about 3 degrees, they would be able to tell the difference, and they made a right triangle with one corner equal to 3 degrees, and based on this triangle they said that the sun had to be at least about 20 times farther away than the moon.)
The Moon's Orbit
Let's pause for a moment and think philosophically about what we've discovered. Everything that we see in the sky rises in the east and sets in the west, once a day. It is as if all of outer space is spinning around us, from east to west, one turn per day. But this may be because we live on a sphere that is spinning from west to east, one turn per day. It would be like looking out at the playground or the park from a spinning Merry-Go-Round.
Like everything else, the moon seems to go in circles around us from east to west once a day … except it is going a little more slowly than everything else. Compared to everything else, the moon is very slowly moving backwards. When we watch the evening moon for several days in a row, we find that it is migrating slowly up from the western horizon, and over towards the eastern horizon. Compared to everything else in outer space, the moon is slowly circling the other way, from west to east. So whether all of outer space is spinning around once a day, or we ourselves are living on a spinning Planet-Go-Round, the moon has its own motion. The moon slowly circles around from west to east once a month, and we can see this happen in the sky. When we watch the crescent moon slowly climb higher over the sunset day-by-day, and then pass through the rest of its phase cycle, we are really watching the moon pass slowly through its orbit.
Eclipses and Spheres in Space
The sun and the moon have their daily and monthly routines. But every once in a while, something dramatic and remarkable happens — the moon or the sun goes dark for an hour or two. We call these rare events “eclipses,” and we can learn a lot about our neighborhood in space by paying attention to these special events. [You may or may not have eclipses coming up this year where you live, but if you do, you should definitely pay attention to them. Otherwise, we can use photographs and records of past eclipses, or maybe we can look through an eclipse catalog on the web. Then we can discuss the different kinds of eclipse, and we can pick a couple of “typical” eclipses to study in detail.]
Eclipses of the Moon
If we were to examine historical records, or maybe visit a webpage that describes upcoming eclipses, we would find that lunar eclipses are not all the same. For example, sometimes all of the moon goes dark, and sometimes only part of it. But there are always certain things in common. Do we ever see a quarter moon that suddenly goes dark? A crescent moon? Here's one important clue to what causes lunar eclipses: they always happen to a full moon, which means the sun and the moon are on opposite sides of the sky. And the moon does not go anywhere unusual in the sky, or stop its daily motion across the sky. The lunar eclipse happens to the moon while it otherwise continues its normal behavior. However, it could happen anywhere along the “highway,” which means at any time of day. It could happen to the moon as it rises in the east in the evening, or as it sets in the west before dawn, or it could happen while the moon is down and the sun is up, in which case we don't get to see it. Let's pick a “typical” eclipse to study, and study the sequence of events in detail. [If there was an eclipse recently, or if there is one coming up soon, you can use that one. Otherwise I recommend just studying a “generic” moonrise (evening) total eclipse. If you'd like a specific example to make the discussion a little more grounded, the next total lunar eclipse will occur in March 2025, and it will be an “evening moonrise” eclipse for the West Coast of the United States. In the Midwest and on the East Coast it will be a “midnight eclipse,” or a bit after midnight, with the moon high in the sky. If you'd like to search for other recent or upcoming eclipses, you can try these eclipse tables.]
A Typical (Evening) Lunar Eclipse — The evening starts out like a normal “full moon night,” with the full moon rising in the east just as the sun sets in the west. But then you start to notice that there is a “bite” taken out of the back side of the moon. (If you remember the “arrow through the moon,” the “first bite” will always be somewhere near the tail of the arrow.) As we watch, the bite grows larger and larger, as if something is moving with the moon across the sky, but a little faster, and it is overtaking the moon from behind. Eventually, it eats up the whole moon and then the moon is gone from the sky. Well, not completely gone. Usually, you can still see the moon, it is just dimmer, like something in shadow. (Here's another important clue to what is causing the eclipse. If it were something blocking our view, we wouldn't be able to see the moon at all.) And not only does the moon go dim, it also becomes colorful, for some reason. (The colors are always different, and they might even change as the eclipse goes on, but they are always in the red-orange-yellow part of the color wheel. Does that remind you of any other natural phenomenon?) Finally, the initial sequence reverses itself. The moon comes back, back-end-first. The last thing you notice is the “last bite” at the front of the moon, and after that we are back to a normal full moon night. It is as if the mysterious dark thing has now completely pulled ahead of the moon, and the moon has emerged from the back side of the dark thing.
Why is this Happening? — So here are our clues: There seems to be a dark thing, moving with the moon along the “highway” across the sky, but a little faster, so it overtakes and passes the moon from behind. The dark thing seems to be a shadow, instead of a solid object blocking our view, because we can still see the moon. And we can only see this shadow when the sun and the moon are on opposite sides of us in the sky. Can you figure out what the dark thing is? If the sun and the moon are on opposite sides of us in the sky, they are also on opposite sides of us in space, aren't they? So if the sun is over there, and we see a shadow over there, what's in the middle that could be casting the shadow?
The Moon's Aim — Now, why do we have different kinds of eclipses? If the moon goes on the far side of us in space every month, why don't we have a lunar eclipse every month? Maybe our shadow is always there, up in the night sky pointing away from the sun, but the moon just doesn't aim very well, and it usually misses the shadow? Our shadow must be huge, but the moon is also really far away, so maybe it is easy to miss the shadow? This could also explain why we sometimes have partial eclipses. Sometimes the moon aims well enough to graze the edge of our shadow, but not well enough to actually go all the way inside the shadow?
The Shadow of Our Home — A lunar eclipse gives us the rare and special chance to see the shadow of our own home, and to see with our own eyes a few facts about the size and shape of our world. When you see our shadow on the moon, what shape is it? We never get to see the whole thing, because it is too large to fit on the surface of the moon, but the edge is always curved. It looks like part of a circle. How big is it? If you use your imagination to picture the whole circle, how many times larger than the moon is it? (The clues provided by lunar eclipses are among the main tools that the Greeks used to figure out that the Earth is round, and to estimate the size of the moon compared to the Earth.) One thing we haven't figured out yet is why our shadow is colored. (The clue is in which colors.)
Eclipses of the Sun
As with lunar eclipses, if we study records of solar eclipses, we find that sometimes only part of the sun goes dark, and sometimes all of it. On rare occasions, the middle of the sun goes dark, but it leaves a glowing ring around the margin, as if whatever is blocking the sunlight isn't quite large enough to cover the whole sun. Also, like lunar eclipses, they could happen at any time of day — while the sun is rising in the east, while it is setting in the west, or in the middle of the night, in which case we don't get to see it. One big difference between lunar and solar eclipses is that half of the world gets to see each lunar eclipse, but only a very small part of the world gets to see each solar eclipse. (That might be another useful clue, at some point.) As we did with lunar eclipses, let's pick a “typical” eclipse, and study the sequence of events in detail. [There will be a solar eclipse in April of 2023, visible across much of Australasia, and another one in October of 2023, visible across a large portion of the Americas. If you live in one of those places, I'd recommend studying your upcoming eclipse in detail. Otherwise, I suggest just using a hypothetical post-sunrise eclipse as your “example” or “typical” eclipse.]
A Typical (Morning) Solar Eclipse — The day starts out like a normal day, with the sun rising in the east. The first thing we notice is a “bite” taken out of the front of the moon. (We need to be using “eclipse glasses” to see this, otherwise there is still too much overpowering glare to notice the shape of the sun. Without eclipse glasses, you might not even know it wasn't a normal day until the sun was almost totally eclipsed.) As we watch, this “bite” grows larger and larger. The sun does not stop its journey across the sky, of course, but continues its normal motion across the sky. It's as if something dark is out there in space, traveling with the sun across the sky, but a little slower, and the sun pulls up to it from behind, and then passes behind the object. It is probably a solid object, because it is able to block the sunlight completely. After an hour or so (if this is a total eclipse), the sun goes completely dark! It's as if day suddenly turns into night! This lasts for a couple minutes, and then the sun stars to come back, front-side first. It is as if the sun is now pulling ahead of the dark object and leaving it behind in the sky. If we pay attention to the size and shape of the dark thing, we see it is round, and very nearly the same size as the sun in the sky.
Why is this Happening? — So a round object, looking to be about the same size as the sun in the sky, and probably a solid object, seems to be passing in front of the sun and blocking it from view. What do you think it could be? Here's our final clue: Where is the moon when a solar eclipse happens? The moon is nowhere to be found anywhere else in the sky. Just as lunar eclipses only happen at the time of a full moon, solar eclipses only happen at the time of a new moon. And if you know your lunar cycle, you know that at the time of the new moon, the moon is supposed to be passing close by the sun in the sky anyway. So now what do you think the dark object is that is causing the solar eclipse?
The Moon's Aim — So again, why do have different kinds of eclipse? The answer can be the same as the one we gave for lunar eclipses: the moon doesn't aim very well. Most months, it swings wide of the sun and we have a normal new moon. Sometimes it just grazes the edge, and we have a partial eclipse. On rare occasions, it aims so well that it passes straight across the sun and gives us a total eclipse. But then what about the “ring of fire” or “annular” eclipses, where the moon isn't quite large enough to cover the entire sun? [The October 2023 solar eclipse will be like this.] Maybe the moon is sometimes slightly closer, and appears slightly larger in the sky, and sometimes it is slightly farther away, and appears slightly smaller? The difference can't be much, or we'd notice the moon getting huge and tiny in the sky. But maybe there is a little difference? Then if we have an eclipse when the moon is a little closer, it will give us a total solar eclipse, and if we have an eclipse when the moon is slightly farther, then it will be an annular eclipse? (Maybe you've heard the press get excited about “supermoons” sometimes. This small change in the apparent size of the moon is what they are talking about.)
A Scale Model of the Three Spheres
You probably won't need much convincing at this point that the Earth, the Moon, and the Sun are all spheres, floating around in space. But how big are they compared to each other? How far apart? If we could leave the Earth, and fly out into outer space, and turn around and look back, what would we see? If we wanted to make a scale model of the three spheres, showing how big they all are compared to each other, and how far apart they are, how big do we need to make the three globes? The Ancient Greeks figured these things out. Let's see if we can figure out for ourselves the right size for a scale model of the Sun, Moon, and Earth, using the same clues.
Clue Review — When we discussed the phases of the moon, we noticed that the sun must be very much farther away (and larger than) the moon. Otherwise we wouldn't see the phase cycle that we actually see. If the sun weren't very, very much farther than the moon, we couldn't see a quarter-moon a quarter-turn from the sun in the sky. When we discussed lunar eclipses, we noticed that we could see our own shadow, that it is round, and that it is a few times larger than the moon. We are almost ready to put all of the clues together and see if we can make a real scale model. We just need a few more clues first.
Size Versus Distance — First of all, if the sun is very, very much farther away than the moon, but they look the same size in the sky, what does this tell you? The sun must also be very, very much larger than the moon, as well. In fact, if they look the same size in the sky, we can reason that their sizes and their distances must be in the same proportion. (When we see solar eclipses, sometimes they are total, and sometimes annular, showing us that sometimes the moon is slightly closer and appears slightly larger than the sun in the sky, and sometimes is slightly farther and appears slightly smaller. But this is just a small wobble, and for the purpose of argument we can just assume that, on average, the moon appears to be exactly the same size as the sun in the sky.) If we use a coin or a ball or something, and place it far enough away so that it appears to be the same size in the sky as the sun and the moon (perhaps by using it to cover up a full moon in the sky), then we can even measure the ratio of distance to size. Based on how large they appear in the sky, we can figure out that the moon and the sun must both be about 100 times farther away than they are wide.
The Earth Itself Versus the Earth's Shadow — From a careful study of lunar eclipses, we can learn that the shadow of the Earth is about three times larger than the moon … but what about the Earth itself? We know from solar eclipses that the shadow of the moon shrinks from the size of the moon down to almost nothing across the distance from the Earth to the moon. (When the moon is a little farther than usual, and we see an annular solar eclipse, it actually shrinks to nothing before it even reaches the Earth. When the moon is a little closer than usual, and there is a total eclipse, the shadow hasn't quite shrunk to nothing, and the small portion of the Earth that lies within the remaining shadow is the portion that gets to see the eclipse.) If we assume that the shadow of the Earth shrinks at the same rate (one moon diameter for each Earth-moon distance), then the Earth must be one moon larger than its own shadow, and therefore the Earth itself is about four times larger than the moon.
The Scale Model — Finally we can assemble all of the puzzle pieces, and discover the big picture: The Sun is at least 20 times larger and farther away than the moon (according to Ancient Greek estimates), or about 400 times larger and farther away than the moon (based on modern precision measurements), and the Earth is about 4 times larger than the moon. And however large the sun and the moon are, they must both be about 100 times that distance away from the Earth. And based on these measurements, we can easily make our scale model. (Although we will have to just imagine the sun. If we have a 1-inch ping-pong ball for the moon, and a 4-inch globe for the Earth, then they will need to be roughly 8-10 feet apart, and the sun would have to be as large as a small room and about a mile away.) If you want to make paper models of the Earth and moon to scale, you can make your own round globes, but polyhedral globes would probably be a little easier to make.
How Big is the Earth? — Eclipses and the phases of the moon give us all the clues we need to figure out how large and how far apart the Earth, the Moon, and the Sun are … compared to each other. By thinking carefully about angles and triangles, we can figure out the ratios of sizes and distances, as the Ancient Greeks did over two millennia ago. But we still don't know how large or how far apart any of these things are in miles, or any other familiar earthly measure. But the Ancient Greeks figured this out, too, and so can we. The key is in the angle at which we see outer space, and how much it changes as we travel. Traveling over a curved surface makes us see outer space from different angles, showing that we are traveling over a curved surface. And how much it changes shows us how far around the curve we have traveled. The Ancient Greeks Eratosthenes and Posidonius both estimated the size of the Earth, the former from the angle of the sun in two different cities, and the latter from the stars that could be seen from two different cities. Eratosthenes was very careful with his data, and his estimate was very close to our modern figures.
The Solar System
If we could fly up into outer space and turn around and look back at our neighborhood in space, what would we see? If we want to create a toy model of the universe around us, what should it look like? We already figured out what a scale model of the sun, the moon, and the Earth should look like, by looking into the sky and by thinking about what we can see. What about the wandering stars? If we want to add these “planets” to our model, can we figure out what they look like, and how big to make them, and how far away to put them?
Do we really need to? Cartoon pictures of the “solar system” have been hanging on kindergarten walls, and have been printed on T-shirts and jigsaw puzzles, for many decades now. You probably already know that the planets are other worlds, like the Earth, but with different sizes and made of different things. You probably already know that the sun is supposed to go in the middle, and that all of the planets are supposed to go in circles around the sun, with the Earth being the third one from the sun. That's what our neighborhood in outer space is supposed to look like.
But how realistic are those cartoons? When we made our first scale model, you may have been a little startled by how far away we had to put the moon from the Earth, and by how large and how far away the sun had to be. Cartoons often show the planets pretty close together … Is that misleading? How large and how far away do we have to put the planets in a realistic scale model? Also, we've been stargazing for a long time now, and hopefully you've been enjoying the beauty of the night sky, and you'll recall the five “wandering stars” that you can see in the night sky. Perhaps you've even tracked the locations of the planets for several months in a row. (If not, you might be able to observe planetary behavior by studying a complete planet calendar.) By paying attention to the planets in the night sky, we can notice some interesting and curious things about the way they move around. So when we watch the planets move around in the night sky, are we really watching changes in the solar system? Can we actually find the solar system in the sky and watch the planets as they orbit the sun? The night sky shows us half of all outer space, so we should be able to see at least part of the solar system on any given night, shouldn't we?
Let's study or review how the planets move in the sky, and then let's see if the solar system actually makes sense, and what a scale model would actually look like.
The Zodiac and the Ecliptic
The “Planet Path” — It is not uncommon to see two or even three planets together over a sunrise or sunset. And whenever we do, they are always lined up. Sometimes we are lucky, and we can see four or five planets together in the same sky, and they form a beautiful arc all the way across the sky. So the planets are never scattered around in the sky like pellets from a shotgun blast, they always fall along a very fine line in the sky, like a narrow “planet path” through the constellations. The planets wander around on the map of outer space, but they can't wander just anywhere. They are confined to this narrow trail, and when they move, they can only move forwards or backwards along the trail. [For most of spring 2023, Mars and Venus will be visible in the evening skies, although Mars will be fairly dim. Starting in May 2023, Jupiter and Saturn will be together over the sunrise.] And the sun and the moon move through the stars along the same path. The next time you see planets over a sunset, use your imagination and the glow on the horizon to picture the sun below the horizon, and see if the sun lines up with the planets. (This might also be a good time to see if you can figure out which constellation the sun is currently in.) The next time you see a crescent moon with planets over a sunset, watch the moon day by day and you will see it march along the “planet path” through the constellations, passing the planets one by one. (When we studied eclipses, we found that the moon doesn't “aim” very well as it travels through the sky. For the same reason, it usually passes the planets to one side, as if it is in the passing lane of the planet path. But sometimes on rare and special occasions, it will “hit” a planet. What do you suppose that looks like?)
The Tilted Planet Circle — This “planet path” is not the same thing as the “solar highway” we talked about earlier, although they are closely related. To recap: the “solar highway” is something we imagine in our own backyard sky. It is a very broad “highway” across our sky from east to west, with shoulders and a centerline. The shoulders are where the sun goes in our sky on the summer and winter solstices, and the centerline is where the sun goes on the equinoxes. The “planet path” is something we have to imagine running through the constellations, on our celestial sphere or our “map of outer space.” To find it, perhaps we can draw marks on our celestial sphere showing all the places we have seen planets. Perhaps we can just try to find it on someone else's map. In any case, if we can find the complete “planet path” on a celestial sphere, we see it forms a complete circle around us. Wherever the sun, the moon, and the planets are in the sky, they will always be somewhere on this circle. The circle is a little like the celestial equator, but tilted. It is as if someone grabbed the equator on two sides, and lifted one side up and pushed the other side down. And this is why the planet path seems to wobble. In your sky, there will always be one end somewhere on the east-ish horizon, and one on the west-ish horizon, but it doesn't run straight from east to west. It wobbles. This is also why the sun, the moon, and all of the planets cross our sky each day along a higher or lower arc, like the sun in different seasons. On the celestial sphere, the tilted planet circle has a high (northern) side, running over Orion's head through Gemini and Taurus. Anything that has wandered along the circle into these constellations will pass across our sky each day along a high arc, like the sun in summer. And on the opposite side of the celestial sphere there is the low (southern) side of the circle, running through Scorpius and Sagittarius. Anything that has wandered along the circle into these constellations will pass across our sky each day along a low arc, like the sun in winter. [As usual, I am assuming you live in the Northern Hemisphere. If you live in the Southern hemisphere, reverse “high” and “low,” and “summer” and “winter.”]
The Zodiac — This “Highway of the Wanderers” or “Planet Ring” seems important. We should probably give it a formal name, and we should carefully mark it on our map of outer space. If we have been studying the constellations for a while, then we have probably already noticed several bright constellations that the planets pass through: Leo, Taurus, Gemini, Scorpius and Sagittarius. We can use these constellations as “landmarks,” showing us the path of the planets through the sky even if there are no planets there. But there are several gaps and dark patches along the circle. If we want to make a complete set of signposts all the way around this circular “racetrack” or “planet ring,” then we'll have to fill in the gaps with some dimmer constellations. We can fill in some of the gaps by naming the very dim constellations Cancer, Aquarius, and Pisces. We probably won't be able to find these constellations in the sky if we live in a city, but they will still be important markers on our map of outer space. There are also a few constellations, like Virgo, that have one or two very bright stars, but the rest of the constellation is dim, so they are hard to recognize. All together, we can name a set of twelve “signs” or markers, like signposts around the circular racetrack, and we use these signs to find the planet ring in the sky, even if no planets are there. We can also use them to monitor the progress of all the planets as they move around the racetrack. (Do you think we'll find that they just move in steady circles around the ring, or will they move in weirder ways?) Since so many of the signs represent animals or people, we call this ring of constellations the “zodiac.” (The name comes from the Greek word for “animal,” which also gives us the words “zoo” and “zoology.” Maybe you can think of this set of signposts that we set up along the planet ring as the “zoo-diac.”)
The Ecliptic — The zodiac is the casual star-gazer's way to find the “planet path” in the sky. But if we want to make measurements, like professional scientists do, we need to be more precise and mathematical. For this, we also name a specific geometric line that runs down the middle of the path, like the centerline of a highway. The planets wobble a little as they move down the highway, and the moon wobbles a lot. But the sun's path is pretty steady. The sun traces out an exact circle through the constellations. So we can use the sun's path as our “centerline.” We can only have eclipses when the moon is also on this line (which it usually isn't), so we call this circle the “ecliptic.” The ecliptic is like the centerline of the zodiac.
Motion in a Plane — If you've been thinking ahead, you can probably already see what this means for the solar system. If you want to find the solar system in the sky, you will need to find the “planet ring.” Any time you can see several planets together in the sky, maybe with the moon, too, and the sun below the horizon, just connect the dots in your imagination. That line-up in the sky is your view of the solar system from your backyard. If you can't see any planets, you will need to search for zodiac constellations, and use those to imagine the circle. If you want to find it on somebody else's map of outer space, you will need to search for the curve labeled “ecliptic.” What about our scale model? How would we need to arrange everything in a model so that, from the viewpoint of the Earth, everything else always appears within the same circle around us? We have to put everything in the same plane in space. Whether everything goes around us on the Earth, or we all go around the sun, all of the motion has to happen in one flat plane. In our scale model, we don't have to worry about tilting any of the circles, and we can arrange them all on the same tabletop or football field. The solar system (or whatever it is) has the shape of a plane, and the “planet ring” is our view of the plane from the inside. Sometimes astronomers call this the “plane of the ecliptic.” If the solar system cartoons are correct, then that circle around us is our view of the solar system, looking out sideways from the inside. And the “plane of the ecliptic” is really the Earth's orbital plane in space. So whenever we can find several planets in the sky, and connect the dots, we are really visualizing the solar system in the sky. Whenever we look at a zodiac constellation, we are looking out sideways through the solar system. (But why is the solar system tilted in such a strange way in the sky? Think back to when we made a map of the moon, and we had to choose the proper “top” and “bottom” for the map. We had to stop thinking about the ground and the horizon where we live, and start comparing the moon to outer space. The solar system in the sky is like that. The tilt of the solar system in our own sky will change depending on where we live on Earth, and also on the season and the time of day. But if we compare the “planet path” and the plane to other things in outer space, we can find a proper “top” and “bottom.” If we make a scale model, we will have to allow our home on Earth to be tilted in a strange way, so that we can turn the solar system right-side-up. To make a model of the solar system in a horizontal plane, we will have to allow our own home on Earth to be off-kilter.)
… or Nearly a Plane — Why does the moon aim so poorly? Why doesn't it “hit” the sun, or the Earth's shadow, or any of the planets along the “planet path” more often? If we follow the motions of the planets through the constellations, we see they also wobble a bit, especially during retrograde motion. Except for the sun, all of the “wanderers” along the “planet path” usually veer away from the centerline a little, as if they are taking a passing lane on the highway. How can we explain this? How do we have to adjust our model to get the moon and the planets to wobble? Perhaps we can just say that that moon and all of the planets have their own orbit circle around the sun, and all of the circles are pretty close to being in the same plane, but not exactly? Each thing has its own orbital plane, and they are all pretty close to the same plane, but not exactly? (To explain eclipses, this means that we have to think about the intersection line between two planes: the ecliptic plane and the slightly tilted plane of the moon's orbit. We can only have eclipses when this line is rotated to coincide with the line connecting the Earth and the sun. When this doesn't happen, the moon lies above or below the plane of the ecliptic, and to us it appears to pass above or below the sun or the Earth's shadow in the sky.)
The Habits of the Planets
So we can explain the “planet path” that we see in the sky simply by saying that the planets are always in the same plane. When we make our model, we can just arrange all of our neighbors in space in the same plane (or nearly so), and make them move only in that plane. If the solar system model is correct, then that circular “planet ring” that we see in the sky is simply our view of the solar system from within the plane of the solar system. But what about the motions of the planets within the plane? By paying careful attention to the motions of the planets along the planet circle (either in person or by studying planet calendars), we discover that all of the planets have their own habits or characteristic way of migrating along the circle, and they aren't so simple as steady motion in one direction. If the solar system model is correct, then we should be able to explain all of the back-and-forth motions of planets along the zodiac as circular motions around the sun, within the plane of the solar system. How does that work? How can circular motions appear to be back-and-forth motions?
The Sun — We can't see the sun and the stars at the same time in the sky, but we can easily figure out where the sun is on our map of outer space simply by paying close attention to sunrises and sunsets. If we do, we discover that the sun does move in a steady circle, from west-to-east, marching day by day along the ecliptic. But this is exactly how it would look if the Earth was going in a steady circle instead of the sun. We are simply seeing the sun from a changing perspective, with different signs of the zodiac in the background, as we circle around the sun in the plane of the ecliptic.
Venus & Mercury — Venus and Mercury only appear over sunrises and sunsets, and we never see them far from the sun in the sky. They hang out over the sunrise for a while, then sink into the sunrise and reappear a little later over the sunset. Then they hang out over the sunset for a while, before swinging back to the sunrise and starting all over again. These two planets just swing back and forth between the sunrise side of the sun and the sunset side. That's their “way of life.” Mercury got its name because it is the fastest planet. It swings between sunrises and sunsets every couple of months. It never rises very high above the sunrise or sunset, and it is also fairly dim, which makes it one of the hardest planets to find. (If you want to go “Mercury hunting,” try to find out when it is at “greatest elongation,” meaning farthest from the sun.) Venus can rise much higher over the sunrise and sunset, and it is also much brighter, brighter than any other star or planet. And it hangs out over sunsets for months at a time, making a beautiful evening scene. If you see a brilliant, beautiful “Evening Star” over the sunset, or a “Morning Star” over the sunrise, it is probably Venus. So how do we have to move the little globes in our model to create this behavior? How can we make them appear to swing back-and-forth around the sun from the Earth's point of view?
Mars, Jupiter, and Saturn — These three planets are not trapped near the sun. We can see them anywhere along the “planet ring” at any time, including far from the sun and high in the sky in the middle of the night. Jupiter is almost as bright as Venus, but unlike Venus it can be seen high in the night sky, like a king of gods looking down on the world. Saturn was named after Chronos, the god of time, because if you watch it move through the constellations, you don't see much activity. Saturn is a “wandering star,” but it is the slowest one (unless you also count the telescopic planets, which are even slower). Mars is distinctly reddish and is usually dim, but occasionally it grows almost as bright as Jupiter, like a god of war flaring up in anger. If we compare these three to the sun, they just creep steadily in circles from east to west. If we watch them in the evening sky, night by night we see them creep a little closer to the sun, until they finally disappear into the sunset. A short time later, we see them reappear over the sunrise, and begin to steadily creep away from the sun. But sometimes these planets act in strange ways. Sometimes we see them on the opposite side of the sky from the sun, where the full moon is. We call this position opposition, and planets can act a little strangely when they are there. For one thing, this is when Mars flares up in anger. (Jupiter and Saturn also grow a little brighter at opposition, but not enough that you would normally notice.) Also, if you are tracking their progress through the constellations instead of comparing them to the sun, you will notice that compared to the constellations, they turn around and move backwards for a while. They go in reverse through the zodiac whenever they are at opposition. We call this “retrograde motion.” (Their motion is always east-to-west if you ignore the stars and compare the planets only to the sunrise or sunset. You only notice retrograde motion if you are tracking their progress through the zodiac. Their normal motion is west-to-east through the zodiac, except during retrograde motion, when they move east-to-west for a little while.)
The View from a Moving Ship — You can probably see that the motion of Venus and Mercury makes perfect sense. In the sky, they appear to travel with the sun through the zodiac, but swing back-and-forth around it, because they are really moving in circles around the sun. When we watch them swing back and forth between sunrises and sunsets, we are really watching them move in sideways circles around the sun. Venus rises higher over the sunrises and sunsets than Mercury does, and takes longer to repeat itself, so Venus' circle must be larger and slower than Mercury's circle. (Do the angles mean anything? With the moon, we were able to do some work with triangles, and figure out some sizes and distances. Can we figure out how large to make the circles for Venus and Mercury in our model, based on how far we can see them from the sun?) The “outer planets” are a little harder. In particular, why do they seem to move backwards through the stars when they are at opposition? Can you figure it out? Maybe it will help to first think about why planets would be brighter when they are at opposition.
A Scale Model of the Solar System
What Do the Planets Look Like? — Until approximately the year 1600, there had been no reason to think that the “wandering stars” were any different from normal stars, except for the fact that they move around. Then Galileo Galilei made a telescope, pointed it into outer space, and saw things that nobody in history had ever seen before. [He wrote about these things in Sidereus Nuncius, which is fairly light reading in translation and is fun to read to students.] In Galileo's telescope, “true” stars were still basically pinpoints of glaring light, but the “wandering” stars were now disks, circles with a measurable size. And in the case of Venus, the disk was only partly there. Galileo discovered that Venus has phases like the moon! So Venus is more like the moon than the sun. It is NOT lit by its own fire, but by the borrowed light of the sun, just like the moon is. Galileo also discovered four completely new wandering stars, unknown to all people before him. And these four new wanderers are all trapped next to Jupiter, and wander back and forth around Jupiter. Jupiter has its own moons! So it had finally been proven that there could be things in outer space that go around something other than the Earth. And as we mentioned when we were talking about the moon, Galileo discovered mountains and plains on the moon. The moon is not smooth, it has a landscape! (Galileo also noticed something strange about Saturn, but Saturn was in a bad viewing position at the time, and the existence of rings would be clearly discovered later.) So the moon and the wandering stars are in fact other worlds. And you can see all of these beautiful things for yourself in any quality telescope.
How Big are the Planets? — With the sun and the moon, we were able to figure out that they are both about 100 times farther away than they are wide, based on how large they appear to be in the sky. Now that we can see the “visual disk” of the planets in a telescope, we could do exactly the same thing. We would just have to know the magnification power of the telescope we are using, and take that into account in our calculations.
How Far Away are the Planets? — If we can do a little work with triangles, as we did when thinking about eclipses, we can easily figure out how far away to put Mercury and Venus from the sun in our model, at least as a fraction or ratio of the distance from the sun to the Earth. We rarely see Mercury more than about 20° from the sun in the sky, which means that we must be about 3 times farther from the sun than the radius of Mercury's circle. Venus can be as much as half of a right angle or about 45° from the sun in the sky, which means that we must be about 1.4 times farther from the sun than the radius of Venus' circle. This also means that Venus' circle is about twice as large as Mercury's circle. The “outer planets” are a little more complicated, but once we have figured out how retrograde motion works, we can use a similar strategy with triangles to figure out how far away to put Mars, Jupiter, and Saturn from the sun in our model.
The Solar System in the Park — Can we finally make a complete scale model of the solar system? Mercury and our own Moon are pretty close to the same size. Let's make these two things the smallest bodies in our model, and let's suppose we could use a one-millimeter BB or pin head to represent them both. This means that our globe for the Earth will need to be about 4mm across. Can you look up the modern measurements for diameter and average orbital radius for everything in the solar system? Can you calculate how large the sun and the other planets would have to be for our scale model, and how far apart you would have to place them, based on a 4mm Earth?