Finding “True North”

Go outdoors and look around. How can you tell which way is north? When I was young, the answer was: “Use a compass.” But if “north” just means “where a compass points,” then why do we talk about “true north”? Is there such a thing as “false north”? And how did the Ancient Egyptians manage to line up their pyramids with north without any compasses at all? Is there a way we can find “true north” all by ourselves, without a compass?

Technology does not give us the cardinal directions. Technology merely helps us to find them. The cardinal directions are fundamentally given to us by nature. If you've spent any amount of time carefully studying the ways of the sun, the moon, and the stars, you may have noticed that there is symmetry in the sky. The sun, the moon, and many of the stars rise on one side, they peak in the middle, and they set on the other side. There is a precise, mathematical line of symmetry running exactly across the middle of the dome of the sky and dividing it into two equal halves, an eastern or “rising” half and a western or “setting” half. This line of symmetry is given to us by astronomy and it is the most important thing that we can use to orient ourselves. We get our bearings and measure directions around us by starting from this line of symmetry. If we want to find “true north,” we need to find this important line of symmetry in the sky.

If you want to find this line of symmetry for yourself, and mark it down onto the ground so you can make your own backyard compass rose, there are several ways you can do it. You can find north either from the sun, or from the stars. But however you do it, it always amounts to finding the line of symmetry in the sky. (If you live in the Northern Hemisphere you can also find true north very nearly by finding the North Star, or Polaris. But there is no such thing as a “South Star” for those of you in the Southern Hemisphere, and in the ancient world there wasn't even a “North Star.” Even in the modern world, the North Star is only very close to true North, and not exactly. So let's see if we can master the skill of finding true symmetric north without relying on an accidental star.) Using the sun is probably more practical for most people, so let's start with that way.

Finding North from the Sun

If you have tracked the path of shadows across the ground, you may have discovered that the path of the shadow of a vertical pole can have different shapes. It might be straight or it might be curved, depending on the season of the year. But it is always symmetric. There is always a point where the path passes closest to the pole, and the shape of the path is symmetric on both sides of that point. If you want to mark the north-south line in the ground, you can do it by drawing this shadow-path on the ground, and then finding the line of symmetry.

If you want to draw a compass rose in your back yard or garden, you could use stakes and ropes for your surveying work. (The Ancient Egyptians invented the art of “rope-stretching” or surveying, and they did their work with stakes and ropes.) For illustration purposes, I used a pencil and a dowel. I bought a blank clock face from a craft store and stuck a sharpened dowel in the center, and then I marked where the shadow of the dowel fell with a pencil.

I lined up the seam in the clock face with the seam in the sidewalk just in case I needed to move the disk and put it back in the same place later. This also allowed me to take the disk indoors to do the geometric work, and then put it back in the same place for my final photo. The final path for one full day looked like this:

You can already notice that the arc is curving slightly. (If you have already seen what shadow paths look like in different seasons, you can probably tell me what season it was when I took these photos.) You'll also notice that the line of symmetry, i.e. the north-south line, is not quite parallel to the seam in the sidewalk. The seam in my sidewalk runs nearly, but not quite, north and south.

The next step is to draw the line of symmetry as best we can. If you just want a crude eyeball estimate, you could just stretch a rope or lay a ruler where you think the centerline lies, crossing both the central pole and the point where the curve comes closest to the pole, and then mark that line. But there is a more precise way to do it. (It is very much like “constructing a perpendicular line” with a compass-and-straightedge construction … which the Egyptians also invented.) If you've ever used a compass and ruler to construct a perpendicular bisector, or to bisect an angle, perhaps you can already see how to do it.

If we draw a circle around the central post, large enough to cut the arc, it will cut the arc in two symmetric places, one on each side of the line of symmetry. If you are doing this in your yard or garden, you can follow the Egyptians and just swing a rope around the central pole, a little like a maypole. If you are doing this indoors, you could use a drawing compass. I just bent a paperclip into a two-sided hook long enough to cross the shadow path, and used that to guide my pencil.

(Another strategy would be to draw one or more circles beforehand, which would save you the trouble of paying attention to the shadow all day long. You would just have to be paying attention at the two times when the shadow crosses the circle, and mark those two locations. But you have to have some sense of when this is going to happen so that you can be present at the right times. If you want to do really precise work, you could also use several circles of different sizes and repeat the procedure several times.)

From this point forward, the problem is exactly the same as bisecting an angle. The two points you just located, when connected to the center, form two symmetric rays, one on each side of the line of symmetry. If we bisect the angle between them, we will have found the North-South line.

If you've never bisected an angle before, you need to draw two circles (or circular arcs) of the same radius around each of the two points you just located. This gives two symmetric circles, one on each side of the centerline, and wherever these two circles intersect each other, those intersection points will lie on the line of symmetry. Unless the circles are too small, they will intersect each other in two places, and the two points of intersection will also line up with the central pole, and all three of these points together will form the line of symmetry. (Technically, you only need two points to form a line, but it's reassuring if you can make all three points line up. If your two intersection points and the central post don't all form a straight line, you know you've done something wrong. On the other hand, if your circles are too large, the outer point of intersection may lie too far away for you to be able to draw it. In that case, you would just use the inner intersection point and the center point to form your line of symmetry.)

Now all you have to do is use a ruler (or a taut rope) to connect the dots, and to draw or etch that line permanently in the ground or in your drawing surface. This line will be like a baseline or a floor line underneath the line of symmetry in the dome of the sky over your head, dividing your world precisely into eastern and western halves, and pointing to “true north.”

This north-south line of symmetry will also be parallel to (or more exactly “coplanar with”) the axis around which the celestial sphere seems to spin. (If it is really the Earth that is spinning, then this north-south line will show you the direction of the Earth's axis.) This is the real meaning of “true north.” This is the direction of your world's spin axis, which creates the rhythm of the day and drives all of the daily rhythms of life on Earth.

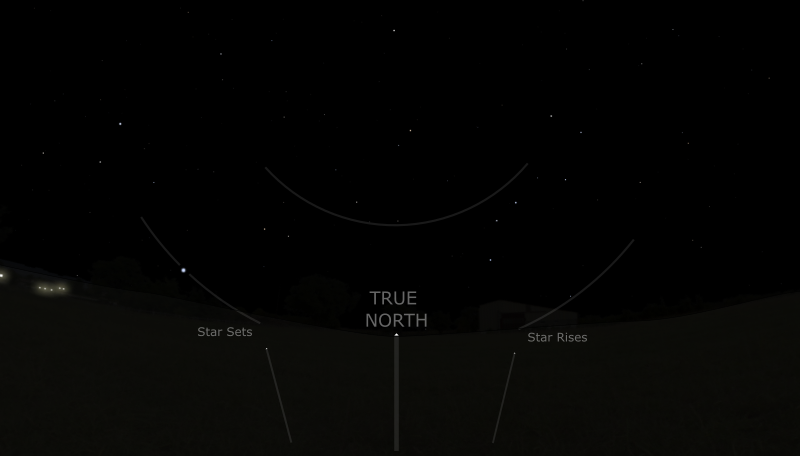
Finding North From the Stars

If you want to be able to orient yourself when you are lost outdoors at night, you just need to learn which are the northern stars. (Or, if you live in the Southern Hemisphere, you need to learn the southern stars.) The northern sky always contains the same stars. Keep the Great Bear on your left, and you'll be sailing east. But what about drawing a perfect line of symmetry in the ground, like we did with the sun? Can we find “true north” from the stars? There was no “North Star” in the ancient world, and yet the Ancient Egyptians still managed to line up their pyramids perfectly with the cardinal directions. (I've read that they used the stars to do this, but to be honest, I don't really know whether they used the sun or the stars. Probably both.)

In any case, you can use a similar procedure to the one we used for the sun. You just pick any star that rises and sets (i.e. not a circumpolar star), and for which you can clearly see the rise and set locations on the horizon. Then you mark the direction in which that star sets, and the direction in which the same star rises, and halfway between these two directions will be the line of symmetry. The rise and set directions form two rays from your central anchor point, and you can bisect the angle to find the central line of symmetry. (You do need to have a fairly clear view of the horizon for this, and the rising and the setting of the star you've chosen might occur during the daytime, in which case you won't be able to see it.) If you'd like to try this method, see if you can use a planisphere to choose a somewhat-northerly star that sets long after the sun goes down tonight, and rises well ahead of the sun tomorrow morning. You could also use the rising and setting of stars in the southern sky, in which case the angle bisector will point south.