Scientific Sundials

If you draw a clock face on a paper plate, place a pencil in the center to cast a shadow, and place the whole thing in the sunshine … will it tell the time? The shadow will definitely move across the clock face as the sun moves across the sky, but will the shadow move in a circle like the hand of a clock? Or will it follow some other path?

If you want to make a scientific, mathematical, geometric sundial, then your “clock” on the ground needs to match and follow the real path of the shadow as it moves. Your “ruler” of hour marks needs to have a shape on the ground that matches the path of the shadow. But what's the right shape? If it isn't a circle, then what could it be? You can easily find out for yourself by following shadows through the course of a day. And since shadows always land on the ground in a place that is opposite to the sun in the sky, then by tracking shadows across the ground you will also be tracking the sun across the sky. You will be able to see the shape of the sun's path across the sky reflected in the shape of the shadow's path across the ground. And once you understand the sun's path across the sky, then you can design all kinds of fancy and beautiful devices to mark and measure the sun's progress across the sky. You can follow the sun through the hours of the day, and also through the seasons of the year, by using shadows. You can make all kinds of beautiful sundials.

(Warning: There are “plot spoilers” ahead. In the discussion below, I'm going to present some of my own results from tracking shadows, so if you want to try that yourself, you may want to do so before you read any further. Or you could read about my results, and then see if you find the same thing where you live, or if you find results that are different from mine.)

What is the shape of the sun's path across the sky?

If you have the ability to make time-lapse videos, you could “speed up” the motion of the shadow, and that would be a great way to watch how shadows (and the sun) move throughout the day. I happen to own an automated time-lapse camera (they aren't too expensive), so I made my own time-lapse videos of the shadow of a vertical stick. I used a blank wooden clock face, with a sharpened dowel in the center, but a blank paper plate with a pencil in the center would work almost as well. (Just make sure the wind doesn't blow it away.)

What do you notice? The shadow always moves across the dial from the western side to the eastern side, as the sun passes across the sky from the east to the west. Does the sun ever go straight overhead? If it did, what would happen to the shadow? There is always a moment in the middle of the day when the shadow is shortest (and it points due north at that moment), but there is never a time of day when the shadow disappears. The sun is highest in the sky at noon, and it comes quite close to being straight overhead at noon in the summer, but at no time does it ever go straight overhead … at least not where I live. What about summer versus winter? Isn't the sun supposed to be higher in summer and lower in winter? You can see this clearly in the paths. In winter, the shadows are always longer, and the path stays far away from the center, because the sun stays much lower in the sky. In summer, the shadows can become very short, and the path passes very close to the center, as the sun passes high across the sky.

Now for the curious part. What about the shapes of the curves? The summer path seems more “normal”, and more like the hand of a clock sweeping around the center. But the equinox path is a straight line (or nearly so), and the winter path is curved the other way, for some strange reason. If we were to sketch out the entire pattern, it would look something like this:

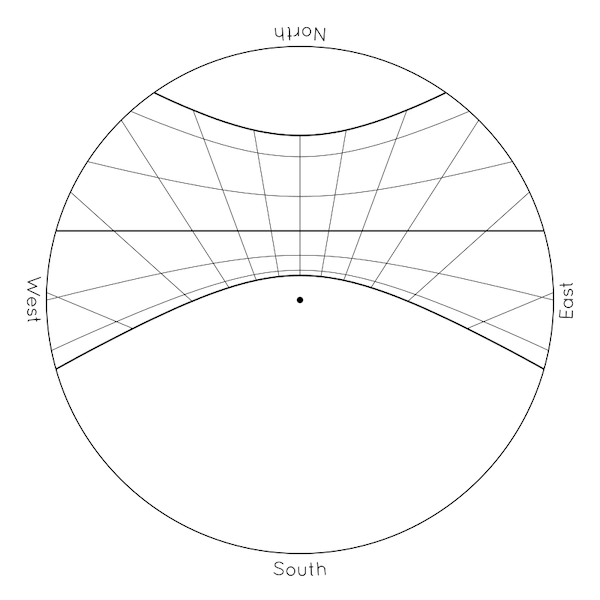
What's going on? We could discuss in more detail why the pattern on a horizontal surface looks the way it does, and make a “gnomonic” or "butterfly sundial." We could also notice that these patterns on the ground give us a way to find true north. But to continue the present discussion, let's come back to the question of the shape of the sun's path in the sky. What do those patterns on the ground mean for the shape of the sun's path across the sky? (If you know what hyperbolas look like, you make recognize the summer and winter paths as hyperbolas. This could be the basis for a fascinating discussion of conic sections, but let's leave that for another day.)

There is a sort of “highway” across the ground from west to east, reflecting or mirroring the sun's “highway” across the sky from east to west, but why is the shape so funny? The problem is that we are trying to take something curved and we are making it appear on something flat. We are trying to record the sun's curved path across the “dome” of the sky on the flat ground. What if we could record the path of the sun across the sky on a curved object instead of a flat one? What if use a bowl instead of a disk? What if we put something in the center of the bowl to cast a shadow, and put it in the sunshine? The shadow of the thing in the center would fall on the side of the bowl at a point exactly opposite to the sun in the sky, wouldn't it? And as the sun moves across the “dome” of the sky, the shadow would move across the bowl in a mirror-image path. We could record the path of the sun across the sky by recording the path of the shadow across the bowl, and the shape of the path would be exactly the same … just upside-down and backwards. We would have a working model of the sky.

Unfortunately, I don't have any time-lapse movies to show of the motion of a shadow across a bowl. Instead, I'm just going to give you a preview of what a “bowl sundial” or “hemispherical sundial” would look like.

As with the flat plate or “horizontal sundial,” there is a broad “highway,” with a curve at both sides for summer and winter, and a curve running down the middle for spring and fall. But this time, it looks much more “normal.” The curves on the bowl are always portions of a circle.

And finally, we can say what the shape of the sun's path across the sky is. If we flip our bowl or upside-down “sky model” upside down and backwards, it will show us the exact geometric path of the sun across the sky in different seasons. A cartoon diagram of the sun's “highway” across my sky would look like this:

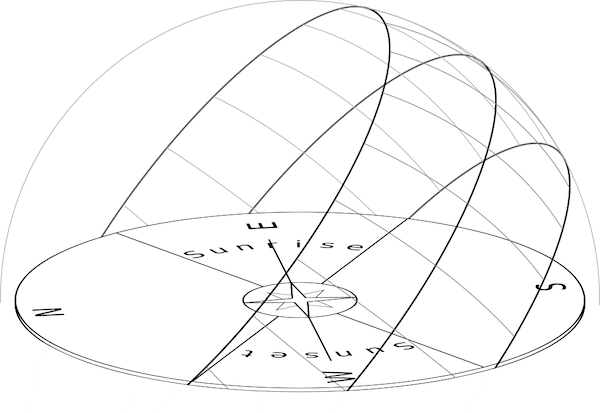
It is as if the sun's daily path is always a circle, with a portion of the circle above the horizon and a portion below the horizon. But the circle shifts to the north in summer and to the south in winter. In summer, more of the circle is above the horizon, and less is below, so the days are longer than the nights. In the winter, more than half of the circle is below the horizon, and less is above, so the nights are longer than the days.

This is what the “solar highway” across the sky looks like in my sky. What about yours?

If you study the path of the sun across the sky in different places of the world, you will discover an identical “highway,” except it will be tilted to different angles. It will stand up straighter as you approach the Equator. (And if you live close enough to the Equator, the sun will actually pass overhead some days of the year.) The “highway” will tilt closer and closer to horizontal as you travel north. At the North Pole, the circles will lie perfectly horizontal. In the Southern Hemisphere, they will be tilted, but they will tilt into the northern sky instead of the southern sky.

So what is the shape of the sun's path across the sky? It is always a circle (or a portion of a circle), except that the circle will be tilted to different angles depending on where you live, and the circle will oscillate north and south as the months of the year pass. If you want to make a scientific sundial, you will need to worry about these two things. You will need to tilt your sundial somehow to match the tilt of the sun's wheel at your latitude, and you will need to be able to follow the sun as the circle shifts throughout the seasons.

Scientific Sundials

I would say that there have been two periods in Western History in which sundials and sundial-makers flourished: the classical world of the Ancient Greeks and Romans, and the “Golden Age of Sundials,” corresponding roughly to the Renaissance and the Enlightenment in European history. Before the Greeks, most early agricultural societies noticed that shadows are longer in the morning and evening, and shorter in the middle of the day, and they used this fact to help them know when to do certain things each day. (Perhaps they came in from the fields for lunch when their shadows were shorter than they were, or something like that.) And sometimes they would even make little devices with marks on them, like the simple “sundials” invented by the Egyptians and Babylonians. (A simple paper plate “clock face” sundial would be like this.) But it was the Greeks who first applied geometry, recorded the path of the sun in the sky as a circle, and divided the day into equal slices of time by dividing the circle of the sun into equal arcs. It was also the Greeks who first realized that each sundial had to be tilted or otherwise adapted to each city's latitude, because the sun's arc in the sky is tilted differently in different cities, and that sundials need different curves if they are to track the sun in different seasons. These ancient masters of geometry and of stone-carving made sun-tracking sundials in the shape of spheres, cones, and cylinders, as well as flat horizontal plates, and they created the first scientific instruments in human history.

Sundials With Calendars

All of the Greek sundials used a metal needle or something similar to cast the shadow of a point onto a grid, and you could read both the time and the season by where the shadow of the point fell on the grid. If you'd like to make a Greek Sundial of your own, I have designed a couple of paper versions of Greek sundials. Perhaps the easiest to understand (but the hardest to make) would be a hemispherical sundial. This kind of sundial uses a hemispherical bowl with a shadow-casting point in the center, and it amounts to an inverted model of the sky. The “solar highway” is reflected from the sky onto the opposite wall of the bowl, with the shorter, higher arc representing the shorter, lower arc of the sun's winter journey across the sky, and the lower, longer arc marking the sun's higher, longer summer journey across the sky.

A much easier to make (but harder to understand) version would be a flat, horizontal sundial. For this, we only have to make a flat horizontal surface with a vertical stick in the middle. But now the markings are messier. For a flat, horizontal sundial, we have to copy that weird “butterfly pattern” onto the surface. If you'd like to make a “gnomonic” or “butterfly” sundial out of paper, it is quite easy, once you have the right design for your latitude.

"Garden Variety" Sundials

Many centuries later, during the “Golden Age of Sundials,” people already knew well how the sun moves through the sky, but they were starting to travel more and have meetings more often. They needed simple, practical time-telling devices more than they needed “sun-tracking” scientific instruments. So they invented simpler, easier to read sundials that ignored the calendar and simply told the time of day. (Clocks had actually been invented by this time, but they were still huge and unreliable. Sometimes towns would have a town clock in a tower somewhere, but they would still need to use sundials to reset the clock to the correct time every day.) But how can you ignore the calendar, and still make sure that your sundial works correctly in every season? The key difference in these sundials is to use an edge to cast a shadow instead of a point or tip of some kind, and to make sure that the stick or the edge that you are using to cast the shadow is not vertical, but is tilted so that it is parallel to the axis of the sun's wheel. The sun's “wheel” has to appear to turn around your edge or stick like an axle. (Or if it is really the Earth that is spinning, then the stick or the edge of your sundial will need to be parallel to the axis of the Earth. In a correctly-made sundial, you should be able to see the axis of the Earth reflected in the tilted gnomon of the sundial.) Using a line instead of a point makes the sundial much easier for a casual user to read, and making sure that the edge is tilted and lined up with the axis means that you don't have to worry about the seasons. The sundial will keep regular time regardless of the season. It was during this era that most familiar “garden variety” sundials appeared, and these are the ones that most people think of today when you say “sundial.”

If you want to make your own “simple” or “garden variety” sundials out of paper, you can try one of my own simple paper sundials, or this paper cube sundial, and you can find many more designs by searching the internet. Rob Ives has an especially nice Equatorial Sundial. You might also try the book Sundials and Timedials, and Sunny Day U.